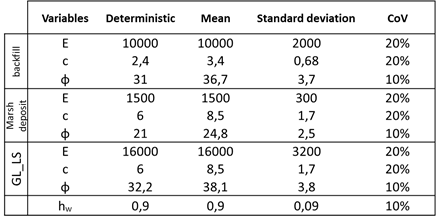
Now, within ZSWalls+R™, it is possible to specify probability density functions (given by (log)normal, Beta, Uniform or Gumbel distributions with means and standard deviations) for the Young’s modulus, the friction angle and the cohesion of every soil, as well as the water table height and the surface loads. Then, a real probabilistic analysis will be possible, propagating the input variables’ uncertainties across ZSWalls™, in order to get probabilistic results such as safety factors, horizontal or vertical displacements and bending moments.

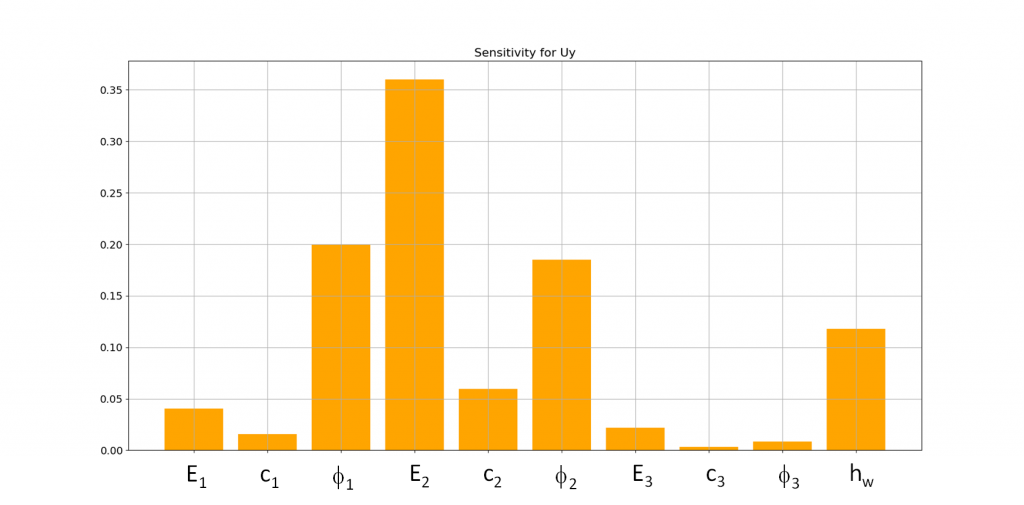
Sensitivity analyses provide a better understanding of the problem, since they make it possible to determine the most influential input variables on the results (displacements, bending moments, safety) and therefore allow to concentrate on the most important parameters. Observe here that f₁, E₂ and f₂ are the most significant parameters for the evaluation of the settlement.

In ultimate state analyses, reliability analyses help determine the probability of failure Pf of a structure as the integral below the probability density function of the safety factor FS, when FS < 1. By analogy, it is also possible to calculate the probability of failure of a system at the serviceability limit state as the integral under the probability density of a displacement d, when d > d(limit).

Looking at the settlement histogram yields Pf(settlement > 3.5 cm) = 7.6%.

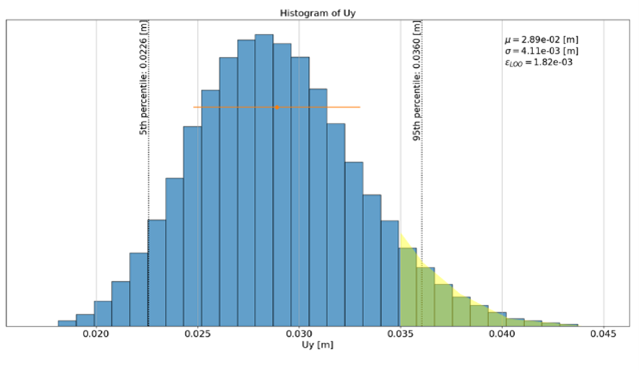
Correlations can be also taken into account. Here, introducing a negative correlation of -0.8 between c and f yields a new Pf(settlement > 3.5 cm) = 5.2%.

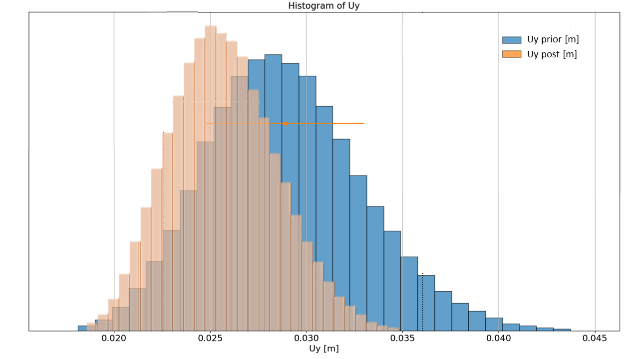
The uncertainties about the result (here a settlement), quantified by the notion of standard deviation, depend greatly on the uncertainties present in the input parameters of the model. It is therefore essential to reduce these uncertainties. For this, two possibilities: multiply the in situ and laboratory tests on soil samples, or use experience and in situ measurements (displacements during execution, water levels, ...) in order to update our calculation hypotheses. The first possibility is always possible, but can be expensive. In addition, the new surveys will not give us an indication of the real value of the solicitations involved (loads, water level, etc.).  The use of Bayesian inference, or inverse analysis, makes it possible to formalize the second possibility with a coherent and generic methodology, in order to refine the measurement of the probability of failure (from a priori to a posteriori), then optimize the design and save money and CO2 if the value of Pf decreases a posteriori.

Here a 1.5 cm horizontal displacement is measured 1 m below the soil’s surface, when the excavation has reached 1.9 m. ZSWalls+R allows you to update the probability that the silo’s settlement will exceed 35 mm, given the new information that we have at hand. Observe that, in our case, Pf reduces drastically and ends being smaller than 0.1 %.